Acid and base

Acid-Base Chemistry

---

Water

We typically talk about acid-base reactions in aqueous-phase environments -- that is, in the presence of water. The most fundamental acid-base reaction is the dissociation of water:

H2O H+ + OH-

In this reaction, water breaks apart to form a hydrogen ion (H⁺) and a hydroxide ion (OH^-). In pure water, we can define a special equilibrium constant (K_w) as follows:

KW = [H+][OH-] = 1.00x10-14

Where K_w is the equilibrium constant for water at 25° C (unitless)
[H⁺] is the molar concentration of hydrogen
[OH^-] is the molar concentration of hydroxide

An equilibrium constant less than one (1) suggests that the reaction prefers to stay on the side of the reactants -- in this case, water likes to stay as water. Because water hardly ionizes, it is a very poor conductor of electricity.

pH

What is of interest in this reading, however, is the acid-base nature of a substance like water. Water actually behaves both like an acid and a base. The acidity or basicity of a substance is defined most typically by the pH value, defined as below:

pH = -log[H⁺] At equilibrium, the concentration of H⁺ is 1.00 × 10^-7, so we can calculate the pH of water at equilibrium as:

pH = -log[H⁺]= -log[1.00 × 10^-7] = 7.00 Solutions with a pH of seven (7) are said to be neutral, while those with pH values below seven (7) are defined as acidic and those above pH of seven (7) as being basic.
pOH gives us another way to measure the acidity of a solution. It is just the opposite of pH. A high pOH means the solution is acidic while a low pOH means the solution is basic.

pOH = -log[OH^-] pH + pOH = 14.00 at 25°C

Definitions of acids and bases

• Arrhenius
  acid: generates [H⁺] in solution
  base: generates [OH^-] in solution
  normal Arrhenius equation: acid + base salt + water
  example: HCl(aq) + NaOH(aq) NaCl(aq) + H₂O(l)
• Brønsted-Lowery:
  acid: anything that donates a [H⁺] (proton donor)
  base: anything that accepts a [H⁺] (proton acceptor)
  normal Brønsted-Lowery equation: acid + base acid + base
  example: HNO₂(aq) + H₂O(aq) NO₂^-(aq)+ H₃O⁺(aq)
  Each acid has a conjugate base and each base has a conjugate acid. These conjugate pairs only differ by a proton. In this example: NO₂^- is the conjugate base of the acid HNO₂ and H₃O⁺ is the conjugate acid of the base H₂O.
• Lewis:
  acid: accepts an electron pair
  base: donates an electron pair
  The advantage of this theory is that many more reactions can be considered acid-base reactions because they do not have to occur in solution.

Salts

A salt is formed when an acid and a base are mixed and the acid releases H⁺ ions while the base releases OH^- ions. This process is called hydrolysis. The pH of the salt depends on the strengths of the original acids and bases:

Acid	Base	Salt pH
strong	strong	pH = 7
weak	strong	pH > 7
strong	weak	pH < 7
weak	weak	depends on which is stronger

These salts are acidic or basic due to their acidic or basic ions. When weak acids or weak bases react with water, they make strong conjugate bases or conjugate acids, respectively, which determines the pH of the salt.

Acid-Base Character

For a molecule with a H-X bond to be an acid, the hydrogen must have a positive oxidation number so it can ionize to form a positive +1 ion. For instance, in sodium hydride (NaH) the hydrogen has a -1 charge so it is not an acid but it is actually a base. Molecules like CH₄ with nonpolar bonds also cannot be acids because the H does not ionize. Molecules with strong bonds (large electronegativity differences), are less likely to be strong acids because they do not ionize very well. For a molecule with an X-O-H bond (also called an oxoacid) to be an acid, the hydrogen must again ionize to form H⁺. To be a base, the O-H must break off to form the hydroxide ion (OH^-). Both of these happen when dealing with oxoacids. Strong Acids: These acids completely ionize in solution so they are always represented in chemical equations in their ionized form. There are only seven (7) strong acids:

HCl, HBr, HI, H₂SO₄, HNO₃, HClO₃, HClO₄ To calculate a pH value, it is easiest to follow the standard "Start, Change, Equilibrium" process.
Example Problem: Determine the pH of a 0.25 M solution of HBr.

Answer:
	HBr (aq)	→	H+(aq)	+	Br-(aq)
Start:	.25 M		0 M		0 M
Change:	-.25		+.25		+.25
Equilibrium:	0		.25		.25
	pH = -log[H+] = -log(.25) = 0.60

Weak Acids: These are the most common type of acids. They follow the equation:

HA(aq) H⁺(aq) + A^-(aq) The equilibrium constant for the dissociation of an acid is known as K_a. The larger the value of K_a, the stronger the acid.

Ka =	[H+][A-] [HA]

Example Problem: Determine the pH of 0.30 M acetic acid (HC₂H₃O₂) with the K_a of 1.8x10^-5.

Answer:

Write an equilibrium equation for the acid:

HC2H3O2 H+ + C2H3O2-

Write the equilibrium expression and the Ka value:

Ka = [H+][C2H3O2-] [HC2H3O2] = 1.8x10-5

"Start, Change, Equilibrium":

HC2H3O2 H+ + C2H3O2-     Start: 0.30 M 0 M 0 M     Change: -x +x +x     Equilibrium: 0.30 - x x x

Substitute the variables (disregard the "-x" because it is so small compared to the 0.30) and solve for [H+]:

Ka = 1.8x10-5 = (x)(x) (.30 - x) = x2 .30

x = [H+] = 2.3x10-3

pH = -log[H+] = 2.64

Strong Bases: Like strong acids, these bases completely ionize in solution and are always represented in their ionized form in chemical equations. There are only eight (8) strong bases:

LiOH, NaOH, KOH, RbOH, CsOH, Ca(OH)₂, Sr(OH)₂, Ba(OH)₂ Example Problem: Determine the pH of a 0.010 M solution of Ba(OH)₂.

Answer:
	Ba(OH)2(aq)	→	Ba2+(aq)	+	2OH-(aq)
Start:	.010 M		0 M		0 M
Change:	-.010		+.010		+.010
Equilibrium:	0		.010		.010
pOH = -log[OH-] = -log(.010) = 1.70
pH = 14.00 - 1.70 = 12.30

Weak Bases: These follow the equation:

Weak Base + H₂O conjugate acid + OH^- example: NH₃ + H₂O NH₄⁺ + OH^- K_b is the base-dissociation constant:

Kb =	[conjugate acid][OH-] [weak base][H2O]

example: Kb =

[NH4+][OH-] [NH3[H2O]

K_a x K_b = K_w = 1.00x10^-14 To calculate the pH of a weak base, we must follow a very similar "Start, Change, Equilibrium" process as we did with the weak acid, however we must add a few steps.
Example Problem: Determine the pH of 0.15 M ammonia (NH₃) with a K_b=1.8x10^-5.

Answer:

Write the equilibrium equation for the base:

NH3 + H2O NH4+ + OH-

Write the equilibrium expression and the Kb value:

Kb = [NH4+][OH2-] [NH3][H2O] = 1.8x10-5

"Start, Change, Equilibrium":

NH3 + H2O NH4+ + OH-     Start: 0.15 M -- 0 M 0 M     Change: -x -- +x +x     Equilibrium: 0.15 - x -- x x

Substitute the variables (disregard the "-x" because it is so small compared to the 0.15) and solve for [OH-]:

Kb = 1.8x10-5 = (x)(x) (.15 - x) = x2 .15

x = [OH-] = 1.6x10-3 M

pOH = -log[OH-] = 2.80

pH = 14.00 - 2.80 - 11.20

When dealing with weak acids and weak bases, you also might have to deal with the "common ion effect". This is when you add a salt to a weak acid or base that contains one of the ions present in the acid or base. To be able to use the same process to solve for pH when this occurs, all you need to change are your "start" numbers. Add the molarity of the ion, which comes from the salt, and then solve the K_a or K_b equation as you did earlier.
Example Problem: Find the pH of a solution formed by dissolving 0.100 mol of HC₂H₃O₂ with a K_a of 1.8x10^-8 and 0.200 mol of NaC₂H₃O₂ in a total volume of 1.00 L.

Answer:
	HC2H3O2(aq)	→	H+(aq)	+	C2H3O2-(aq)
Start:	.10 M		0 M		.20 M
Change:	-x		+x		+x
Equilibrium:	.10 - x		x		.20 + x
Ka = 1.8x10-8 = (x)(.20 + x) (.10 - x) = (x)(.20) (.10)
x = [H+] = -9.0x10-9
pH = -log(9.0x10-9) = 8.05

Acid-Base Titrations

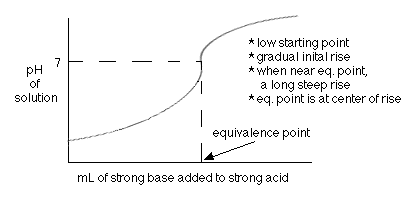
An acid-base titration is when you add a base to an acid until the equivalence point is reached which is where the number of moles of acid equals the number of moles of base. For the titration of a strong base and a strong acid, this equivalence point is reached when the pH of the solution is seven (7) as seen on the following titration curve:
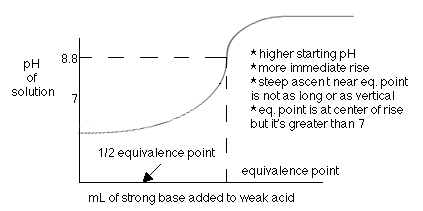
For the titration of a strong base with a weak acid, the equivalence point is reached when the pH is greater than seven (7). The half equivalence point is when half of the total amount of base needed to neutralize the acid has been added. It is at this point where the pH = pK_a of the weak acid.
In an acid-base titration, the base will react with the weak acid and form a solution that contains the weak acid and its conjugate base until the acid is completely gone. To solve these types of problems, we will use the K_a value of the weak acid and the molarities in a similar way as we have before. Before demonstrating this way, let us first examine a short cut, called the Henderson-Hasselbalch Equation. This can only be used when you have some acid and some conjugate base in your solution. If you only have acid, then you must do a pure K_a problem and if you only have base (like when the titration is complete) then you must do a K_b problem.

pH = pKa + log

[base] [acid]

Where:
pH is the log of the molar concentration of the hydrogen
pK_a is the equilibrium dissociation constant for an acid
[base] is the molar concentration of a basic solution
[acid] is the molar concentration of an acidic solution

Example Problem: 25.0 mL of 0.400 M KOH is added to 100. mL of 0.150 M benzoic acid, HC₇H₅O₂ (K_a=6.3x10^-5). Determine the pH of the solution.

Answer:

Determine where in the titration we are:

0.400 M x 0.025 L = 0.0100 mol KOH added

0.150 M x 0.100 L = 0.0150 mol HC7H5O2 originally

because only 0.100 mol of base has been added, that means the thitration is not complete; this means there are two ways to solve this problem: the normal way and the way using the Henderson-Hasselbalch Equation.

Normal way:

HC7H5O2 + OH- C7H5O2- + H2O     before reaction: 0.015 mol 0.0100 mol 0 mol --     change: -0.0100 -0.0100 +0.0100 --     after reaction: 0.0050 0 0.0100 --

Ka = [H+][C7H5O2-] [HC7H5O2] = 6.3x10-5 = (x)(0.0100) 0.0050

x = [H+] = 3.2x10-5 M

pH = -log(3.2x10-5) = 4.49

Henderson-Hasselbalch Way:

[HC7H5O2] = 0.0050 mol 0.125 L = 0.040 M

[C7H5O2-] = 0.0100 mol 0.125 L = 0.0800 M

pH = pKa + log [base] [acid]

pH = -log(6.3x10-5) + log 0.0800 0.0400 = 4.20 + 0.30 = 4.50

This equation is used frequently when trying to find the pH of buffer solutions. A buffer solution is one that resists changes in pH upon the addition of small amounts of an acid or a base. They are made up of a conjugate acid-base pair such as HC₂H₃O₂/C₂H₃O₂^- or NH₄⁺/NH₃. They work because the acidic species neutralize the OH^- ions while the basic species neutralize the H⁺ ions. The buffer capacity is the amount of acid or base the buffer can neutralize before the pH begins to change to a significant degree. This depends on the amount of acid or base in the buffer. High buffering capacities come from solutions with high concentrations of the acid and the base and where these concentrations are similar in value.

problem and solution about acid &base

1. Why is the color of acid-base indicator to change color?

because the reaction of the substance contained in the indicator substance.
not only can digunakasn litmus paper as indicator, man hibiscus Dapa also be used. Acid-base indicator of hibiscus flower, when in acid solution will give a red color, in the base solution will give a green color and the neutral solution is colorless.

2. How do I separate the mixture of base and acid ...?

if a mixture of acid and strong base clearly can not be separated anymore, because cations are very weak and anionnya not hydrolyzed

example NaOH + HCl ---> NaCl + H2O
Na + + H20 - / -> (not responding)
Cl-+ H2O - / -> (not responding)

but when a mixture of weak acids and bases, may be separated by cation / anionnya strong enough and can be hydrolyzed

Example 2 NH4OH + H2CO3 -> (NH4) 2CO3 + 2 H2O
NH4 + + H2O ---> NH3 + H3O +
CO3 ^ 2 - + H2O ---> H2CO3 + OH-

 

Acid and base

Acids and Bases

An Introduction

For thousands of years people have known that vinegar, lemon juice and many other foods taste sour. However, it was not until a few hundred years ago that it was discovered why these things taste sour - because they are all acids. The term acid, in fact, comes from the Latin term acere, which means "sour". While there are many slightly different definitions of acids and bases, in this lesson we will introduce the fundamentals of acid/base chemistry.

In the seventeenth century, the Irish writer and amateur chemist Robert Boyle first labeled substances as either acids or bases (he called bases alkalies) according to the following characteristics:

Acids taste sour, are corrosive to metals, change litmus (a dye extracted from lichens) red, and become less acidic when mixed with bases.

Bases feel slippery, change litmus blue, and become less basic when mixed with acids.

While Boyle and others tried to explain why acids and bases behave the way they do, the first reasonable definition of acids and bases would not be proposed until 200 years later.

In the late 1800s, the Swedish scientist Svante Arrhenius proposed that water can dissolve many compounds by separating them into their individual ions. Arrhenius suggested that acids are compounds that contain hydrogen and can dissolve in water to release hydrogen ions into solution. For example, hydrochloric acid (HCl) dissolves in water as follows:

HCl

H2O

H+(aq)

+

Cl-(aq)

Arrhenius defined bases as substances that dissolve in water to release hydroxide ions (OH-) into solution. For example, a typical base according to the Arrhenius definition is sodium hydroxide (NaOH):

NaOH

H2O

Na+(aq)

+

OH-(aq)

The Arrhenius definition of acids and bases explains a number of things. Arrhenius's theory explains why all acids have similar properties to each other (and, conversely, why all bases are similar): because all acids release H⁺ into solution (and all bases release OH^-). The Arrhenius definition also explains Boyle's observation that acids and bases counteract each other. This idea, that a base can make an acid weaker, and vice versa, is called neutralization.

Neutralization

As you can see from the equations, acids release H⁺ into solution and bases release OH^-. If we were to mix an acid and base together, the H⁺ ion would combine with the OH^- ion to make the molecule H₂O, or plain water:

H+(aq)

+

OH-(aq)

H2O

The neutralization reaction of an acid with a base will always produce water and a salt, as shown below:

Acid		Base		Water		Salt
HCl	+	NaOH		H2O	+	NaCl
HBr	+	KOH		H2O	+	KBr

Though Arrhenius helped explain the fundamentals of acid/base chemistry, unfortunately his theories have limits. For example, the Arrhenius definition does not explain why some substances, such as common baking soda (NaHCO₃), can act like a base even though they do not contain hydroxide ions.

In 1923, the Danish scientist Johannes Brønsted and the Englishman Thomas Lowry published independent yet similar papers that refined Arrhenius' theory.  In Brønsted's words, "... acids and bases are substances that are capable of splitting off or taking up hydrogen ions, respectively."  The Brønsted-Lowry definition broadened the Arrhenius concept of acids and bases.

The Brønsted-Lowry definition of acids is very similar to the Arrhenius definition, any substance that can donate a hydrogen ion is an acid (under the Brønsted definition, acids are often referred to as proton donors because an H⁺ ion, hydrogen minus its electron, is simply a proton).

The Brønsted definition of bases is, however, quite different from the Arrhenius definition.  The Brønsted base is defined as any substance that can accept a hydrogen ion.  In essence, a base is the opposite of an acid.  NaOH and KOH, as we saw above, would still be considered bases because they can accept an H⁺ from an acid to form water.  However, the Brønsted-Lowry definition also explains why substances that do not contain OH^- can act like bases.  Baking soda (NaHCO₃), for example, acts like a base by accepting a hydrogen ion from an acid as illustrated below:

Acid		Base				Salt
HCl	+	NaHCO3		H2CO3	+	NaCl

In this example, the carbonic acid formed (H₂CO₃) undergoes rapid decomposition to water and gaseous carbon dioxide, and so the solution bubbles as CO₂ gas is released.

pH

Under the Brønsted-Lowry definition, both acids and bases are related to the concentration of hydrogen ions present.  Acids increase the concentration of hydrogen ions, while bases decrease the concentration of hydrogen ions (by accepting them).  The acidity or basicity of something, therefore, can be measured by its hydrogen ion concentration.

In 1909, the Danish biochemist Sören Sörensen invented the pH scale for measuring acidity.  The pH scale is described by the formula:

pH = -log [H+] Note: concentration is commonly abbreviated by using square brackets, thus [H+] = hydrogen ion concentration.  When measuring pH, [H+] is in units of moles of H+ per liter of solution.

For example, a solution with [H⁺] = 1 x 10^-7 moles/liter has a pH equal to 7 (a simpler way to think about pH is that it equals the exponent on the H⁺ concentration, ignoring the minus sign). The pH scale ranges from 0 to 14. Substances with a pH between 0 and less than 7 are acids (pH and [H⁺] are inversely related - lower pH means higher [H⁺]). Substances with a pH greater than 7 and up to 14 are bases (higher pH means lower [H⁺]). Right in the middle, at pH = 7, are neutral substances, for example, pure water. The relationship between [H⁺] and pH is shown in the table below alongside some common examples of acids and bases in everyday life.

	[H+]	pH	Example
Acids	1 X 100	0	HCl
	1 x 10-1	1	Stomach acid
	1 x 10-2	2	Lemon juice
	1 x 10-3	3	Vinegar
	1 x 10-4	4	Soda
	1 x 10-5	5	Rainwater
	1 x 10-6	6	Milk
Neutral	1 x 10-7	7	Pure water
Bases	1 x 10-8	8	Egg whites
	1 x 10-9	9	Baking soda
	1 x 10-10	10	Tums® antacid
	1 x 10-11	11	Ammonia
	1 x 10-12	12	Mineral lime - Ca(OH)2
	1 x 10-13	13	Drano®
	1 x 10-14	14	NaOH

asam-basa

Teori Asam dan Basa

Teori asam dan basa Arrhenius

Teori

• Asam adalah zat yang menghasilkan ion hidrogen dalam larutan.
• Basa adalah zat yang menghasilkan ion hidroksida dalam larutan.

Penetralan terjadi karena ion hidrogen dan ion hidroksida bereaksi untuk menghasilkan air.

Pembatasan teori

Asam hidroklorida (asam klorida) dinetralkan oleh kedua larutan natrium hidroksida dan larutan amonia. Pada kedua kasus tersebut, kamu akan memperoleh larutan tak berwarna yang dapat kamu kristalisasi untuk mendapatkan garam berwarna putih – baik itu natrium klorida maupun amonium klorida.

Keduanya jelas merupakan reaksi yang sangat mirip.

Pada kasus natrium hidroksida, ion hidrogen dari asam bereaksi dengan ion hidroksida dari natrium hidroksida – sejalan dengan teori Arrhenius.

Akan tetapi, pada kasus amonia, tidak muncul ion hidroksida sedikit pun!

anda bisa memahami hal ini dengan mengatakan bahwa amonia bereaksi dengan air yang melarutkan amonia tersebut untuk menghasilkan ion amonium dan ion hidroksida.

Teori asam dan basa Bronsted-Lowry

Teori

• Asam adalah donor proton (ion hidrogen).
• Basa adalah akseptor proton (ion hidrogen).

Hubungan antara teori Bronsted-Lowry dan teori Arrhenius

Teori Bronsted-Lowry tidak berlawanan dengan teori Arrhenius – Teori Bronsted-Lowry merupakan perluasan teori Arrhenius.

Ion hidroksida tetap berlaku sebagai basa karena ion hidroksida menerima ion hidrogen dari asam dan membentuk air.

Asam menghasilkan ion hidrogen dalam larutan karena asam bereaksi dengan molekul air melalui pemberian sebuah proton pada molekul air.

Ketika gas hidrogen klorida dilarutkan dalam air untuk menghasilkan asam hidroklorida, molekul hidrogen klorida memberikan sebuah proton (sebuah ion hidrogen) ke molekul air. Ikatan koordinasi (kovalen dativ) terbentuk antara satu pasangan mandiri pada oksigen dan hidrogen dari HCl. Menghasilkan ion hidroksonium, H₃O⁺.

Ketika asam yang terdapat dalam larutan bereaksi dengan basa, yang berfungsi sebagai asam sebenarnya adalah ion hidroksonium. Sebagai contoh, proton ditransferkan dari ion hidroksonium ke ion hidroksida untuk mendapatkan air.

reaction and mechanism

l  Potential Energy and Covalent Bonds

è         Potential energy in molecules is stored in the form of chemical bond energy

è         Enthalpy DH^o  is a measure of the change in bond energies in a reaction

è         Exothermic reactions

H       DH^o is negative and heat is evolved

H       Potential energy in the bonds of reactants is more than that of products

è         Endothermic reactions

H       DH^o is positive and heat is absorbed

H       Potential energy in the bonds of reactants is less than that of products

Problem:

How the relationship between potential energy and covalent bonds?

The solution:

So far, a simple description of covalent bond is a pair of points which are divided between two atoms. Directional nature of covalent bonds have a very strong and has a particular shape that is usually fixed shape even though the substance had experienced physical changes, such as strength or melt.

There are two approaches is important to know how the formation of chemical bonds based on quantum mechanics. One such approach is called the valence bond theory, which allows us to keep using an atomic picture of what we know to form a covalent bond.
1. Valence bond theory is defined as follows: When two atoms form a covalent bond, one of the atomic orbitals overlap (overlap) with other atomic orbitals.
2. Two of the spinning electron pairs can be divided between the two overlapping orbitals, electron density is concentrated between the nucleus of atoms that form a bond.
3. Covalent bond strength, measured in terms of energy when broken down, in proportion to the amount of orbital overlap, the overlapping degree of increase in size, growing stronger ties and increased slightly the potential energy of atoms, when a bond is formed. As a result tend to be in a position to form atomic orbitals overlap in the maximum amount.